ADC 中的量化噪声和幅度量化误差

噪声模型何时会得出有效结果？

我们可以很容易地找到量化误差是可预测的并且不会充当噪声源的示例。例如，如果量化器的输入是DC值，则量化误差将是恒定的。作为另一个示例，假设输入的幅度始终位于量化器的两个相邻量化级别之间。在这种情况下，量化误差等于输入减去DC值。

当输入是正弦波并且量化器的采样频率是输入频率的倍数时，会出现另一个有趣的情况。下面的图 1 展示了一个示例。

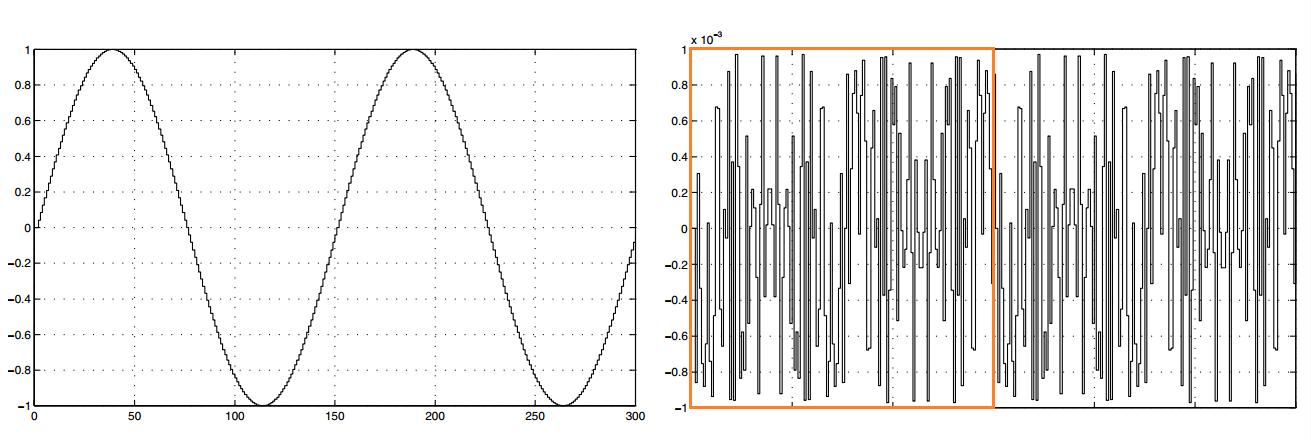
图 1.图片由Data Converters提供。

图 1 的左侧曲线描绘了 10 位量化正弦波的两个周期。右曲线显示了量化误差。对于本例，采样频率与输入频率的比率为 150。

对量化误差的目视检查揭示了周期性行为（一个周期由橙色矩形表示）。正如您所看到的，输入和误差信号之间存在相关性，而噪声源与输入不相关。在这种情况下，我们预计误差信号在输入谐波处具有相当大的频率分量。

误差信号与上述示例中的噪声不同。然而，在许多实际应用中，例如语音或音乐，输入是复杂的信号，并且表现出以某种不可预测的方式发生的快速波动。在这种情况下，误差信号很可能充当噪声源。

实验测量和理论研究表明，如果满足以下四个条件，将量化误差建模为噪声源是有效的：

输入以相同的概率接近不同的量化级别值（在上面讨论的一些有问题的示例中，我们看到输入总是接近某些特定的量化级别）。

量化误差与输入不相关。

量化器具有大量量化级别（例如当我们有高分辨率 ADC 时）。

量化步骤是统一的（与电话中使用的具有对数特性的数据转换器不同）。

您可以在《离散时间信号处理》一书的第 4.8.3 节中找到表达这些条件的更正式的方式。

如果满足这些必要条件，我们可以用加性噪声源替换误差信号，如图 2 所示。这使我们能够使用信噪比 (SNR) 等概念来表征量化误差的影响。然而，在此之前，我们需要找到噪声源的统计模型。

图2

量化噪声的统计模型

表征噪声源的步可以是估计给定值可能出现的频率。这种幅度分布可以通过长时间观察噪声信号并采样以创建幅度直方图来获得。直方图由多个箱组成，这些箱对应于跨越噪声幅度的整个可能范围的连续幅度间隔。bin 的高度表示 bin 间隔内的样本数。

让我们看一下量化噪声直方图的示例。假设输入是离散余弦信号x[n]=0.99cos(n/10)（如图3所示）。

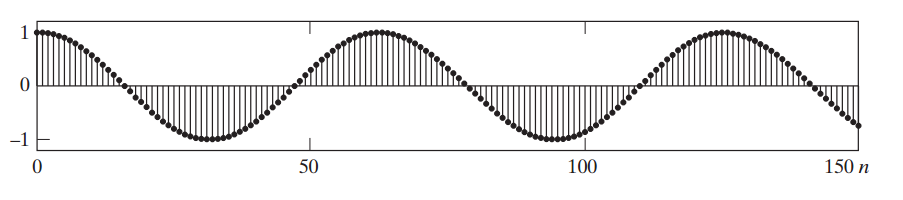
图 3. 图片由离散时间信号处理提供。

如果我们对该信号应用 8 位量化器，量化误差序列将如图 4 所示。

图 4.图片由离散时间信号处理提供。

量化噪声幅度分布

现在，我们从误差信号中获取 101,000 个样本，并构建一个具有 101 个 bin 的直方图，这些 bin 表示范围从 -LSB/2 到 +LSB/2 的幅度间隔。

结果如下图5所示。

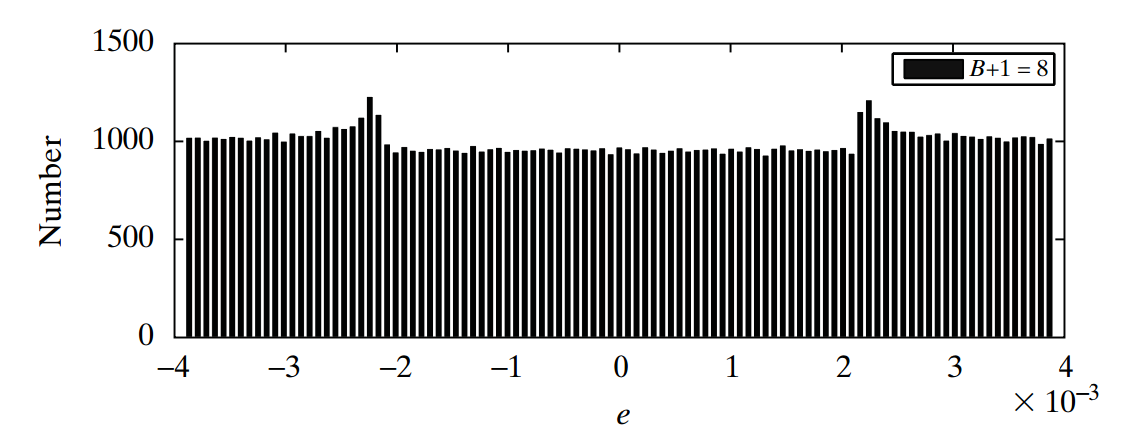
图 5.图片由离散时间信号处理提供。

如您所见，本例中的LSB/2 约为 4×10 -3 。

有趣的是，不同 bin 间隔中的样本数量几乎相同；bin 的高度接近样本总数 (101,000) 除以 bin 数量 (101)。换句话说，噪声幅度均匀分布在±LSB/2之间。如果我们提高量化器分辨率，我们将获得更加均匀的幅度分布。这与有效噪声模型的第三个先决条件是一致的。

虽然我们检查了输入类型和量化器分辨率的特定情况下的直方图，但结果对于量化误差充当噪声源的其他情况也是有效的。因此，我们可以假设噪声幅度是均匀分布在±LSB/2之间的随机变量。

概率密度函数如图 6 所示。

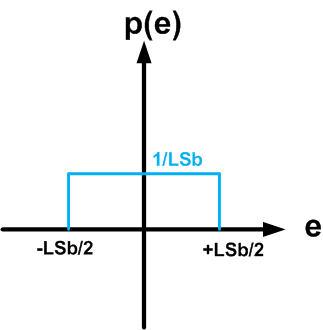
图6

量化噪声可以取±LSB/2之间的值，并且概率密度函数在此范围内恒定（即，它是均匀分布）。由于概率密度函数的积分等于 1，因此当 -LSB/2 < e < LSB/2 时，其值为 1/LSB（参见图 6）。

现在，我们可以计算量化噪声的时间平均功率：

公式1

当噪声信号均匀分布在 ±LSB/2 之间时，该方程给出了量化噪声功率。正如您所看到的，增加量化器的分辨率将降低 LSB 和噪声功率。请注意，该方程与我们（在上一篇文章中）获得的斜坡输入量化误差的 RMS 值一致。

量化噪声功率谱密度

噪声源的另一个重要参数是功率谱密度，它指示噪声功率如何在不同频带中传播。为了找到功率谱密度，我们需要计算噪声自相关函数的傅里叶变换。

假设噪声样本彼此不相关，我们可以在时域中用δ函数来近似自相关函数。由于 delta 函数的傅立叶变换等于 1，因此功率谱密度将与频率无关。因此，量化噪声是总功率等于LSB 2 /12的白噪声。

为了找到奈奎斯特间隔（DC 到 f采样/2）上的单侧功率谱密度 S 一侧( f) ，我们应该将噪声功率除以 f采样/2。因此，

量化如何降低信噪比？

现在我们知道了量化噪声的功率和功率谱密度，我们可以使用图2的模型来分析量化过程。例如，假设我们有一个 N 位量化器，其满量程值用 FS 表示。如果我们将正弦波 $$\frac{FS}{2}sin(2\pi ft)$$ 应用到量化器，量化器输出的 SNR 会是多少？输出将是输入正弦波加上量化过程产生的一些噪声。所需的信号功率可以计算为量化器？输出将是输入正弦波加上量化过程产生的一些噪声。所需的信号功率可以计算为

量化噪声的功率由公式 1 给出。我们只需要用 $$\frac{FS}{2^N}$$ 替换 LSB。因此，噪声功率为。

_因此，噪声功率为为F S 2 N

SNR 由以下等式给出：

代入数值，我们得到

这导致以下表达式：

公式2

这是一个重要的方程，当输入是具有可能幅度 (FS/2) 的正弦波时，它使我们能够确定理想 N 位量化器的 SNR。例如，根据公式 2，我们知道 10 位 ADC 的 SNR 约为 60 dB。请注意，分辨率每增加一位，SNR 就会增加 6.02 dB。

公式 2 仅考虑量化噪声。如果系统中存在任何其他噪声源，SNR 将低于公式 2 的预测值。例如，虽然我们预计 10 位 ADC 的 SNR 约为 60 dB，但电子元件的噪声可能会导致 SNR 较低。假设此类额外噪声源将 10 位 ADC 的 SNR 降低至 55.94 dB。

在这种情况下，我们可以将 ADC SNR 代入公式 2 来确定 ADC 的有效分辨率，通常称为“有效位数”(ENOB)。

因此，如果 10 位 ADC 的 SNR 为 55.94 dB，则其 ENOB 为 9 位。

一点，请记住，方程 2 是通过假设感兴趣的频带是奈奎斯特间隔而推导出来的。如果输入信号的带宽低于奈奎斯特频率，我们可以仅从量化器输出中选择感兴趣的频带，并提高数据转换器的有效信噪比。